Das vestibuläre Labyrinth
Veröffentlicht: 16.08.2012
Veröffentlicht: 16.08.2012
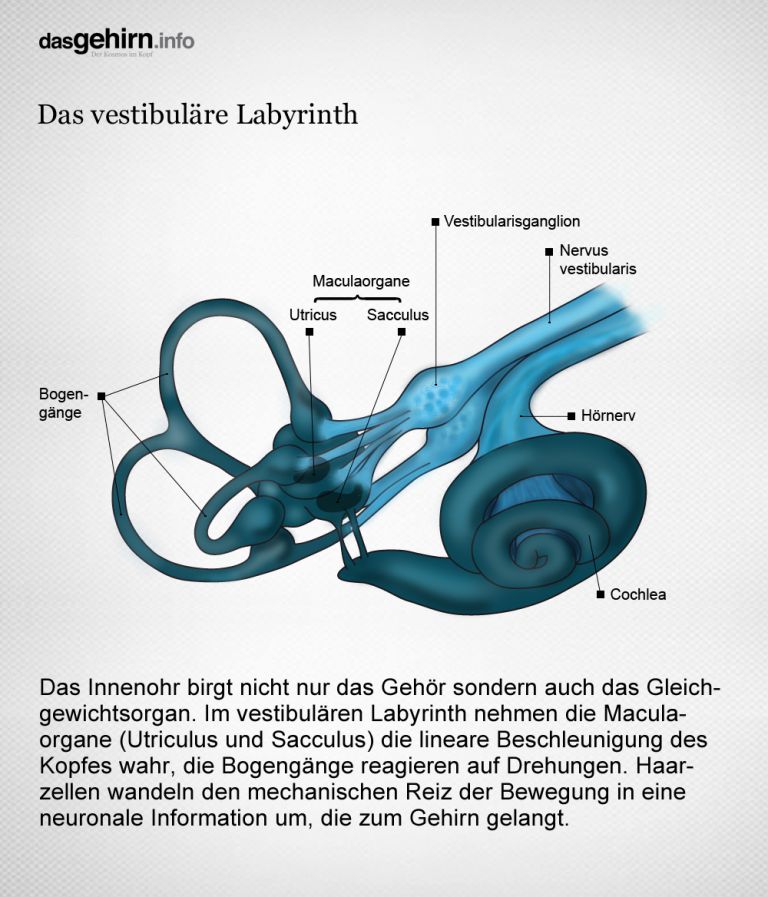
Das vestibuläre System sorgt für Balance und einen stabilen Blick. Die Maculaorgane (Utriculus und Sacculus) registrieren die lineare Beschleunigung des Kopfes, die Bogengänge seine Drehungen.
Lesen Sie mehr dazu in unserem Beitrag Ein Labyrinth fürs Gleichgewicht.
Maculaorgan/Macula statica/macula organs
Gemeinsam mit den Bogengängen bilden die Maculaorgane den Gleichgewichtsapparat im Innenohr von Wirbeltieren. Sie bestehen aus zwei senkrecht zueinander stehenden Strukturen, dem Sacculus und dem Utriculus. Diese Ausrichtung versetzt die Maculaorgane in die Lage, geradlinige Beschleunigungen des Körpers im Raum in allen drei Raumachsen wahrzunehmen: unten-oben, vorne-hinten, links und rechts.
Bogengänge/Ductus semicircularis/semicircular canals
Die Bogengänge sind drei untereinander verbundene, flüssigkeitsgefüllte Schläuche, die nahezu rechtwinklig zueinander stehen und zum Gleichgewichtsorgan gehören. Sie dienen der Registrierung von Winkelbeschleunigungen.
Maculaorgane
Maculaorgan/Macula statica/macula organs
Gemeinsam mit den Bogengängen bilden die Maculaorgane den Gleichgewichtsapparat im Innenohr von Wirbeltieren. Sie bestehen aus zwei senkrecht zueinander stehenden Strukturen, dem Sacculus und dem Utriculus. Diese Ausrichtung versetzt die Maculaorgane in die Lage, geradlinige Beschleunigungen des Körpers im Raum in allen drei Raumachsen wahrzunehmen: unten-oben, vorne-hinten, links und rechts.
Bogengänge
Bogengänge/Ductus semicircularis/semicircular canals
Die Bogengänge sind drei untereinander verbundene, flüssigkeitsgefüllte Schläuche, die nahezu rechtwinklig zueinander stehen und zum Gleichgewichtsorgan gehören. Sie dienen der Registrierung von Winkelbeschleunigungen.
Vestibularapparat
Vestibularapparat/Organon vestibulare/vestibular organ
Das Gleichgewichtsorgan ist Teil des Innenohres. Es hat seine Sensoren in den Bogengängen. Als Teil des Gleichgewichtssystems spürt er kreisförmige Umdrehungen (Rotationen), Beschleunigung und Schwerkraft (Gravitation) auf.
Themen
Tags